Integrals of Trigonometric Functions .

on
In mathematics, the trigonometric integrals are a family of integrals which involve trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.

Sine integral

The different sine integral definitions are:
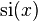{\rm Si}(x) = \int_0^x\frac{\sin t}{t}\,dt
{\rm si}(x) = -\int_x^\infty\frac{\sin t}{t}\,dt
So by definition, {\rm Si}(x) is the primitive of \sin x/x which is zero for x=0 and {\rm si}(x) is the primitive of \sin x/x which is zero for x=\infty. The relation is given by
{\rm Si}(x) - {\rm si}(x) = \int_0^\infty\frac{\sin t}{t}\,dt = \frac{\pi}{2},
where the last integral is known as the Dirichlet integral. Note that \frac{\sin t}{t} is the sinc function and also the zeroth spherical Bessel function.
In signal processing, the oscillations of the Sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency domain ringing if using a truncated sinc filter as a low-pass filter.
The Gibbs phenomenon is a related phenomenon: thinking of sinc as a low-pass filter and the Sine integral as its convolution with the Heaviside step function, it corresponds to truncating the Fourier series, which causes the Gibbs phenomenon.

Cosine integral

.
The different cosine integral definitions are:
{\rm Ci}(x) = \gamma + \ln x + \int_0^x\frac{\cos t-1}{t}\,dt
{\rm ci}(x) = -\int_x^\infty\frac{\cos t}{t}\,dt
{\rm Cin}(x) = \int_0^x\frac{1-\cos t}{t}\,dt
{\rm ci}(x) is the primitive of \cos x/x which is zero for x=\infty. We have:
{\rm ci}(x)={\rm Ci}(x)\,
{\rm Cin}(x)=\gamma+\ln x-{\rm Ci}(x)\,

Hyperbolic sine integral

The hyperbolic sine integral:
{\rm Shi}(x) = \int_0^x\frac{\sinh t}{t}\,dt = {\rm shi}(x).
{\rm Shi}(x)=\sum_{n=0}^\infty \frac{x^{2n+1}}{(2n+1)^2(2n)!}=x+\frac{x^3}{3!\cdot3}+\frac{x^5}{5!\cdot5}+\frac{x^7}{7! \cdot7}+\cdots.

Hyperbolic cosine integral

The hyperbolic cosine integral:
{\rm Chi}(x) = \gamma+\ln x + \int_0^x\frac{\cosh t-1}{t}\,dt = {\rm chi}(x)
where \gamma is the Euler–Mascheroni constant.

Nielsen's spiral

The spiral formed by parametric plot of si,ci is known as Nielsen's spiral. It is also referred to as the Euler spiral, the Cornu spiral, a clothoid, or as a linear-curvature polynomial spiral. The spiral is also closely related to the Fresnel integrals. This spiral has applications in vision processing, road and track construction and other areas.

Expansion

Various expansions can be used for evaluation of Trigonometric integrals, depending on the range of the argument.

Asymptotic series (for large argument)

{\rm Si}(x)=\frac{\pi}{2} - \frac{\cos x}{x}\left(1-\frac{2!}{x^2}+\frac{4!}{x^4}-\frac{6!}{x^6}\cdots\right) - \frac{\sin x}{x}\left(\frac{1}{x}-\frac{3!}{x^3}+\frac{5!}{x^5}-\frac{7!}{x^7}\cdots\right)

{\rm Ci}(x)= \frac{\sin x}{x}\left(1-\frac{2!}{x^2}+\frac{4!}{x^4}-\frac{6!}{x^6}\cdots\right) -\frac{\cos x}{x}\left(\frac{1}{x}-\frac{3!}{x^{3}}+\frac{5!}{x^5}-\frac{7!}{x^7}\cdots\right)
These series are asymptotic and divergent, although can be used for estimates and even precise evaluation at ~{\rm Re} (x) \gg 1~.

Convergent series

{\rm Si}(x)= \sum_{n=0}^\infty \frac{(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}=x-\frac{x^3}{3!\cdot3}+\frac{x^5}{5!\cdot5}-\frac{x^7}{7! \cdot7}\pm\cdots
{\rm Ci}(x)= \gamma+\ln x+\sum_{n=1}^{\infty}\frac{(-1)^{n}x^{2n}}{2n(2n)!}=\gamma+\ln x-\frac{x^2}{2!\cdot2}+\frac{x^4}{4! \cdot4}\mp\cdots
These series are convergent at any complex ~x~, although for |x|\gg 1 the series will converge slowly initially, requiring many terms for high precisions.

Relation with the exponential integral of imaginary argument

The function
{\rm E}_1(z) = \int_1^\infty \frac{\exp(-zt)}{t}\,{\rm d} t \qquad({\rm Re}(z) \ge 0)
is called the exponential integral. It is closely related to Si and Ci:
{\rm E}_1( {\rm i}\!~ x) = i\left(-\frac{\pi}{2} + {\rm Si}(x)\right)-{\rm Ci}(x) = i~{\rm si}(x) - {\rm ci}(x) \qquad(x>0)
As each involved function is analytic except the cut at negative values of the argument, the area of validity of the relation should be extended to {\rm Re}(x)>0. (Out of this range, additional terms which are integer factors of \pi appear in the expression).
Cases of imaginary argument of the generalized integro-exponential function are
\int_1^\infty \cos(ax)\frac{\ln x}{x} \, dx = -\frac{\pi^2}{24}+\gamma\left(\frac{\gamma}{2}+\ln a\right)+\frac{\ln^2a}{2} +\sum_{n\ge 1}\frac{(-a^2)^n}{(2n)!(2n)^2},
which is the real part of
\int_1^\infty e^{iax}\frac{\ln x}{x} \, dx = -\frac{\pi^2}{24} + \gamma\left(\frac{\gamma}{2}+\ln a\right)+\frac{\ln^2 a}{2}-\frac{\pi}{2}i(\gamma+\ln a) + \sum_{n\ge 1}\frac{(ia)^n}{n!n^2}.

Similarly
\int_1^\infty e^{iax}\frac{\ln x}{x^2}dx =1+ia[-\frac{\pi^2}{24}+\gamma\left(\frac{\gamma}{2}+\ln a-1\right)+\frac{\ln^2 a}{2}-\ln a+1 -\frac{i\pi}{2}(\gamma+\ln a-1)]+\sum_{n\ge 1}\frac{(ia)^{n+1}}{(n+1)!n^2}.  

To Join Ajit Mishra's Online Classroom  CLICK HERE 

Comments

Post a Comment