"Relation between Exponential Function & Complex Number" by Ajit Mishra's Online Classroom

on

Relationship to exponential function and complex numbers

Euler's formula illustrated with the three dimensional helix, starting with the 2-D orthogonal components of the unit circle, sine and cosine (using θ = t ).
It can be shown from the series definitions that the sine and cosine functions are the imaginary and real parts, respectively, of the complex exponential function when its argument is purely imaginary:
e^{i\theta} = \cos\theta + i\sin\theta. \,
This identity is called Euler's formula. In this way, trigonometric functions become essential in the geometric interpretation of complex analysis. For example, with the above identity, if one considers the unit circle in the complex plane, parametrized by e ix, and as above, we can parametrize this circle in terms of cosines and sines, the relationship between the complex exponential and the trigonometric functions becomes more apparent.
Euler's formula can also be used to derive some trigonometric identities, by writing sine and cosine as:
\sin\theta = \frac{e^{i \theta} - e^{-i \theta}}{2i} \;
\cos\theta = \frac{e^{i \theta} + e^{-i \theta}}{2} \;
Furthermore, this allows for the definition of the trigonometric functions for complex arguments z:
\sin z = \sum_{n=0}^\infty \frac{(-1)^{n}}{(2n+1)!}z^{2n+1} = \frac{e^{i z} - e^{-i z}}{2i}\, = \frac{\sinh \left( i z\right) }{i}
\cos z = \sum_{n=0}^\infty \frac{(-1)^{n}}{(2n)!}z^{2n} = \frac{e^{i z} + e^{-i z}}{2}\, = \cosh \left(i z\right)
where i 2 = −1. The sine and cosine defined by this are entire functions. Also, for purely real x,
\cos x = \operatorname{Re}(e^{i x}) \,
\sin x = \operatorname{Im}(e^{i x}) \,
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of their arguments.
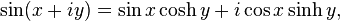
\sin (x + iy) = \sin x \cosh y + i \cos x \sinh y,\,
\cos (x + iy) = \cos x \cosh y - i \sin x \sinh y.\,
This exhibits a deep relationship between the complex sine and cosine functions and their real (sin, cos) and hyperbolic real (sinh, cosh) counterparts.

To Join Ajit Mishra's Online Classroom . Please  CLICK HERE .

Comments

Post a Comment